CAÍDA LIBRE

CAÍDA LIBRE

El movimiento de los cuerpos en caída libre (por la acción de su propio peso) es una forma de rectilíneo uniformemente acelerado. La distancia recorrida (d) se mide sobre la vertical y corresponde, por tanto, a una altura que se representa por la letra h.

En el vacío el movimiento de caída es de aceleración constante, siendo dicha aceleración la misma para todos los cuerpos, independientemente de cuales sean su forma y su peso.

La presencia de aire frena ese movimiento de caída y la aceleración pasa a depender entonces de la forma del cuerpo. No obstante, para cuerpos aproximadamente esféricos, la influencia del medio sobre el movimiento puede despreciarse y tratarse, en una primera aproximación, como si fuera de caída libre.

La aceleración en los movimientos de caída libre, conocida como aceleración de la gravedad, se representa por la letra g y toma un valor aproximado de 9,81 m/s2  (algunos usan solo el valor 9,8 o redondean en 10).

Si el movimiento considerado es de descenso o de caída, el valor de g resulta positivo como corresponde a una auténtica aceleración. Si, por el contrario, es de ascenso en vertical el valor de g se considera negativo, pues se trata, en tal caso, de un movimiento decelerado.

Para resolver problemas con movimiento de caída libre utilizamos las siguientes fórmulas:

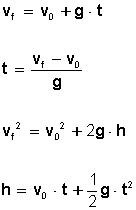
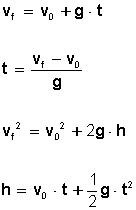
Algunos datos  o consejos para resolver problemas de caída libre: 

Recuerda que cuando se informa que “Un objeto se deja caer” la velocidad inicial será siempre igual a cero  (v0 = 0).

En cambio, cuando se informa que “un objeto se lanza” la velocidad inicial será siempre diferente a cero (vo ≠ 0). Si se lanza hacia arriba la velocidad inicial será positiva y si se lanza hacia abajo la velocidad inicial será negativa.

Tomado de:

http://www.profesorenlinea.cl/fisica/Movimiento_caida_libre.html, el 27 de junio de 2013 a las 14:18.

 

Resolveremos en Modellus el siguiente ejercicio:

A partir del reposo, desde cierta altura, se deja caer una manzana. Dos segundos después se lanza una pelota hacia abajo desde la misma altura de donde se dejó caer la manzana con una velocidad de 28m/s. ¿En qué instante y a qué distancia la pelota alcanza la manzana?

Veamos...